Fortran90 Hofstadter's butterfly．六方格子系に垂直磁場．

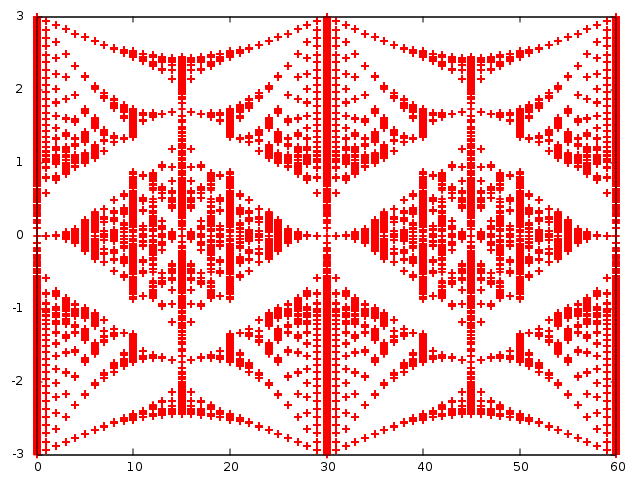
六方格子系に垂直に磁場を与えることでHofstadter's butterflyが現れる．昔かいたFortranコードを発掘したのでアップロード．自然界に現れるフラクタル構造って良いですよね．ちなみに，Hofstadter's butterflyは六方格子系以外の系に垂直磁場を与えてもみられます．

作ったハミルトニアンをLapackで対角化しています．

program zheevtest
  implicit none
  integer,parameter :: d=60
  integer,parameter :: N = 2*d*d             !対角化したい行列の次元
  integer :: lda,lwork,info
  character :: jobz,uplo
  complex(8),dimension(n,n) :: H,work 
  real(8),dimension(n) :: rwork,w

  real(8) :: t,onsite,alpha,beta,gamma,delta,phi1,phi2,B,x1,x2,Pi
  integer :: i,j,p,q,r,s,x,y,u,v,sgn1,sgn2,np
  
  interface
     function chr(p,q)
       implicit none
       integer :: chr
       integer :: p,q
     end function chr

     function trans(p,q,sgn)
       implicit none
       real :: trans
       integer,intent(in) :: p,q,sgn
     end function trans
  end interface

  jobz='N'                !Nで固有値のみ計算。Vで固有ベクトルも計算
  uplo='U' ; lda=n ;  lwork=2*n-1   
  Pi=3.14159265359
   t=-1.0d0
  
  open(17,file="zheev.txt", status="replace")

Do  np=0,d
  write(*,*) np 
  B=8.0*Pi*np/(3.0d0*sqrt(3.0)*d*1.0d0)    
     
Do x=0,d-1
 Do y=0,d-1
  Do sgn1=1,2
   Do u=0,d-1
    Do v=0,d-1
     Do sgn2=1,2

        x1=3.0*(x+y)/2.0
        x2=3.0*(x+y)/2.0+1.0
        
        phi1=sqrt(3.0)*B*(x1-1.0/4.0)/2.0
        phi2=sqrt(3.0)*B*(x2+1.0/4.0)/2.0
        alpha=cos(phi1)*chr(sgn1,1)*chr(x,u)*chr(y-1,v)*chr(2,sgn2)+cos(phi1)*chr(sgn1,1)*chr(x-1,u)*chr(y,v)*chr(2,sgn2)+chr(sgn1,1)*chr(x,u)*chr(y,v)*chr(2,sgn2)
         beta=cos(phi2)*chr(sgn1,2)*chr(x,u)*chr(y+1,v)*chr(1,sgn2)+cos(phi2)*chr(sgn1,2)*chr(x+1,u)*chr(y,v)*chr(1,sgn2)+chr(sgn1,2)*chr(x,u)*chr(y,v)*chr(1,sgn2)
        gamma=sin(phi1)*chr(sgn1,1)*chr(x,u)*chr(y-1,v)*chr(2,sgn2)-sin(phi1)*chr(sgn1,1)*chr(x-1,u)*chr(y,v)*chr(2,sgn2)
        delta=-sin(phi2)*chr(sgn1,2)*chr(x,u)*chr(y+1,v)*chr(1,sgn2)+sin(phi2)*chr(sgn1,2)*chr(x+1,u)*chr(y,v)*chr(1,sgn2)
        onsite=chr(sgn1,1)*chr(x,u)*chr(y,v)*chr(1,sgn2) - chr(sgn1,2)*chr(x,u)*chr(y,v)*chr(2,sgn2)

        H( d*d*(sgn1-1)+x*d+y+1 ,d*d*(sgn2-1)+u*d+v+1 )= cmplx(t*(alpha+beta)+0*onsite,t*(gamma+delta))
       
              End Do
           End Do
        End Do
     End Do
   End Do
End Do
        
  call zheev ( jobz , uplo , n , H, lda, w, work, lwork,rwork,info)

  Do p=1,N
   write(17,*) np,w(p)
  End Do
End Do

close(17)

end program zheevtest


function chr(p,q)
  implicit none
  integer :: chr
  integer,intent(in) :: p,q
  integer :: d
  
   if(p==q .or. p==q+60 .or. p==q-60 ) then
      chr=1
   else 
      chr=0
   end if

return
end function chr

function trans(p,q,sgn)
  implicit none
  integer :: trans
  integer,intent(in)::p,q,sgn
  integer :: d
  d=60
  
if(sgn==1) trans = p*d+q+1
if(sgn==2) trans = d*d+p*d+q+1
    
return
end function trans