Julia言語 多値のカーネル回帰
通常,カーネル重回帰では入力がベクトル,出力がスカラーの関数を学習する訳ですが,入力も出力もベクトルにしたいことがあります.そんなときに使える手法を次の文献で勉強しました.
いろいろ調べても実装している人がいないっぽいので自分で実装した.丸一日かかってしまった...
using LinearAlgebra function kernel_function(kernel) if kernel == "rbf" return (x,y,c,deg) -> exp( -c*norm(x.-y)^2 ) elseif kernel == "lapras" return (x,y,c,deg) -> exp(-c*sum( abs.(x .- y))) elseif kernel == "poly" return (x,y,c,deg) -> (c+x'*y)^deg elseif kernel == "linear" return (x,y,c,deg) -> (0+x'*y)^1 elseif kernel == "periodic" return (x,y,c,deg) -> exp(deg* cos(c * norm(x .- y))) else error("Kernel $kernel is not defined") end end function Kernel(X::Matrix, Y::Matrix; c=1.0, deg=3.0, kernel="rbf") kf = kernel_function(kernel) d, n = size(X) d, m = size(Y) K = Matrix{Float64}(undef, m, n) for j = 1:n for i = 1:m K[i,j] = kf(Y[:,i],X[:,j],c,deg) end end return K end function Kernel(X::Matrix; c=1.0, deg=3.0, kernel="rbf") kf = kernel_function(kernel) d, n = size(X) K = Matrix{Float64}(undef, n, n) for j = 1:n for i = 1:j K[i,j] = kf(X[:,i],X[:,j],c,deg) end end return Symmetric(K) end function vecKernel(X::Matrix, dim_output::Int; c=1, deg=3.0, omega=0.5, kernel="rbf", block_kernel="ones") kf = kernel_function(kernel) _, n = size(X) K = Matrix{Float64}(undef, n*dim_output, n*dim_output) for j = 1:n for i = 1:j K[(i-1)*dim_output+1:i*dim_output,(j-1)*dim_output+1:j*dim_output] = ( kf(X[:,i], X[:,j],c,deg) * block_kernel_A(X[:,i], X[:,j], dim_output, block_kernel, c, omega) ) end end return Symmetric(K) end function vecKernel(X::Matrix, Y::Matrix; c=1, deg=3.0, omega=0.5, kernel="rbf", block_kernel="ones") kf = kernel_function(kernel) dim_input, n = size(X) dim_output, m = size(Y) K = Matrix{Float64}(undef, m*dim_output, n*dim_output) for j = 1:n for i = 1:m K[(i-1)*dim_output+1:i*dim_output,(j-1)*dim_output+1:j*dim_output] = ( kf(Y[:,i], X[:,j],c,deg) * block_kernel_A(Y[:,i], X[:,j], dim_output, block_kernel, c, omega) ) end end return K end """ The matrix `A` represent the relation between output elements. If `A` is `I`, the outputs are independent. """ function block_kernel_A(xi::Vector, xj::Vector, dim_output::Int, block_kernel, c, omega) if block_kernel == "id" A = Matrix{Float64}(I,dim_output,dim_output) elseif block_kernel == "ones" A = ones(Float64, dim_output, dim_output) elseif block_kernel == "ones_id" A = ( omega*ones(Float64, dim_output, dim_output) .+ (1-omega*dim_output)*Matrix{Float64}(I, dim_output, dim_output)) elseif block_kernel == "df" @assert dim_output == size(xi)[1] "df is available only when dim of input and output are same" A = block_kernel_df(xi,xj,c=c) elseif block_kernel == "cf" @assert dim_output == size(xi)[1] "cf is available only when dim of input and output are same" A = block_kernel_cf(xi,xj,c=c) else error("block kernel $block_kernel is not defined") end return A end """ Divergence-free kernel. The dim of output variable and input variable have to be same. The variance 1/σ^2 = c """ function block_kernel_df(xi::Vector, xj::Vector; c=1) m = size(xi)[1] dx = xi .- xj normdx_2 = norm(dx)^2 A = 2*c*(2*c*(dx*dx')+(m-1-2*c*normdx_2)*I) return A end """ Curl-free kernel. The dim of output variable and input variable have to be same. The variance 1/σ^2 = c """ function block_kernel_cf(xi::Vector, xj::Vector; c=1) m = size(xi)[1] dx = xi .- xj A = 2*c*( Matrix{Float64}(I,m,m) - 2 * c * (dx * dx')) return A end """ Vector-valud function learning with kernel method. See the following references, [Mauricio Alvarez et al.](https://ieeexplore.ieee.org/document/8187598) [Luca Baldassare et al.](https://link.springer.com/article/10.1007/s10994-012-5282-y) Learn the projection f(x) : x -> y, where both of x and y are vectorvalued. Let us assume x is in R^k, y is in R^d. n is the number of the training data. k is the number of the test data. # Arguments - 'X_train' : k \times n matrix, training data of input - 'Y_train' : d \times n matrix, training data of output - 'X_test' : d \times m matrix, test data of input. - 'kernel' : 'rbf','lapras','poly','linear','periodic' - 'block_kernel' : 'id', 'ones', 'df', 'cf'. if you chouse 'id', the elements of output are independent each other. - 'lambda' : the value of regularization paramter """ function multiKreg(X_train, Y_train, X_test; kernel="rbf", block_kernel="df", lambda=1.0, c=1.0, deg=3.0, omega=0.5) # dim of output variable d = size(X_train)[1] # number of test data n = size(X_test)[2] K_train_train = vecKernel(X_train, d, c=c, deg=deg, omega=omega, kernel=kernel, block_kernel=block_kernel) K_train_test = vecKernel(X_train, X_test, c=c, deg=deg, omega=omega, kernel=kernel, block_kernel=block_kernel) # in the original paper, they define # c_vec = (K_train_train + lambda*n*I) \ Y_train[:] c_vec = (K_train_train + lambda*I) \ Y_train[:] Y_pred = K_train_test * c_vec Y_pred = reshape(Y_pred, (:,n)) return Y_pred end
k(xi,xj)は,入力ベクトル間の内積で,block_kernel_Aで求めておく行列Aは,出力変数間の関係性の強さを表している.
Aが単位行列(=id)だと,出力変数は全て独立になる.性質の良いAとして,Divergence-freeのものと,Curl-freeのものが知られているのでこれも実装しておいた.
この2つは,入力ベクトルと出力ベクトルの次元が同じじゃないと使えないので注意.
ones_idは以下の論文の5-2-2節で出てくるもので,単位行列と1行列の和.よく使われるのかは分からないけど,とりあえず実装しておいた.
普通のカーネル法を出力する各変数について独立に適用して学習するカーネル回帰はこちら.
using LinearAlgebra function Kreg(X_train, Y_train, X_test;lambda=1, c=1, deg=3.0, kernel="rbf") K_train_train = Kernel(X_train, c=c, deg=deg, kernel=kernel) k_train_test = Kernel(X_train, X_test, c=c, deg=deg, kernel=kernel) # number of test data M = size(X_test)[2] # number of target variables N = size(Y_train)[1] Y_pred = zeros(N,M) for n = 1:N alpha = (K_train_train + lambda * I) \ Y_train[n,:] Y_pred[n,:] .= k_train_test * alpha end return Y_pred end
適当なベクトル場を作って,学習してみる.学習に使った要素は1000個.テストには500個つかった. evalはコスト関数.カーネルの種類をかえてテストしてみる.
using Distributions function eval(y_test, y_pred) L = length(y_test) cost = norm(y_test[:] .- y_pred[:])^2 / L return cost end function make_vector_field(L) f(x,y) = [x+y, x*cos(y)] dist = Uniform(-2, 2) x = rand(dist,(2, L)) y = Matrix{Float64}(undef, 2, L) for i = 1:L y[:,i] = f(x[:,i]...) end return x, y end x_train, y_train = make_vector_field(1000) x_test, y_test = make_vector_field(500) y_pred = multiKreg(x_train, y_train, x_test, kernel="rbf", block_kernel="ones_id" ,lambda=1, c=1, omega=0.5) @show eval(y_pred, y_test) #eval(y_pred, y_test) = 0.5828929693931735 y_pred = multiKreg(x_train, y_train, x_test, kernel="rbf", block_kernel="df" ,lambda=1, c=1, omega=0) @show eval(y_pred, y_test) #eval(y_pred, y_test) = 0.31864270183369753 y_pred = multiKreg(x_train, y_train, x_test, kernel="rbf", block_kernel="cf" ,lambda=1, c=1, omega=0) @show eval(y_pred, y_test) #eval(y_pred, y_test) = 0.052348540778465624
なお,ones_idでomega=0とした場合は,Aが単位行列になるので,各出力変数について独立に学習することに等しい.
実際,Kregと比較してみるとコスト関数は全く同じになる.
y_pred = multiKreg(x_train, y_train, x_test, kernel="rbf", block_kernel="one_id" ,lambda=1, c=1, omega=0) @show eval(y_pred, y_test) #eval(y_pred, y_test) = 0.003875811228195186 y_pred = multiKreg(x_train, y_train, x_test, kernel="rbf", block_kernel="id" ,lambda=1, c=1, omega=0) @show eval(y_pred, y_test) #eval(y_pred, y_test) = 0.003875811228195186 y_pred = Kreg(x_train, y_train, x_test, lambda=1, c=1, kernel="rbf") @show eval(y_pred, y_test) #eval(y_pred, y_test) = 0.003875811228195175
なお,学習したベクトル場を描画したいときは次のようにするとよい.
using Plots using GRUtils y_pred = multiKreg(x_train, y_train, x_test, kernel="rbf", block_kernel="cf" ,lambda=1, c=1, omega=0.0) @show eval(y_pred, y_test) GRUtils.quiver(x_test[1,:], x_test[2,:], y_pred[1,:], y_pred[2,:], arrowscale=1) GRUtils.savefig("predict.png") GRUtils.quiver(x_test[1,:], x_test[2,:], y_test[1,:], y_test[2,:], arrowscale=1) GRUtils.savefig("test.png")
これで推測されたベクトル場predict.pngと,正解のベクトル場test.pngが求まった.
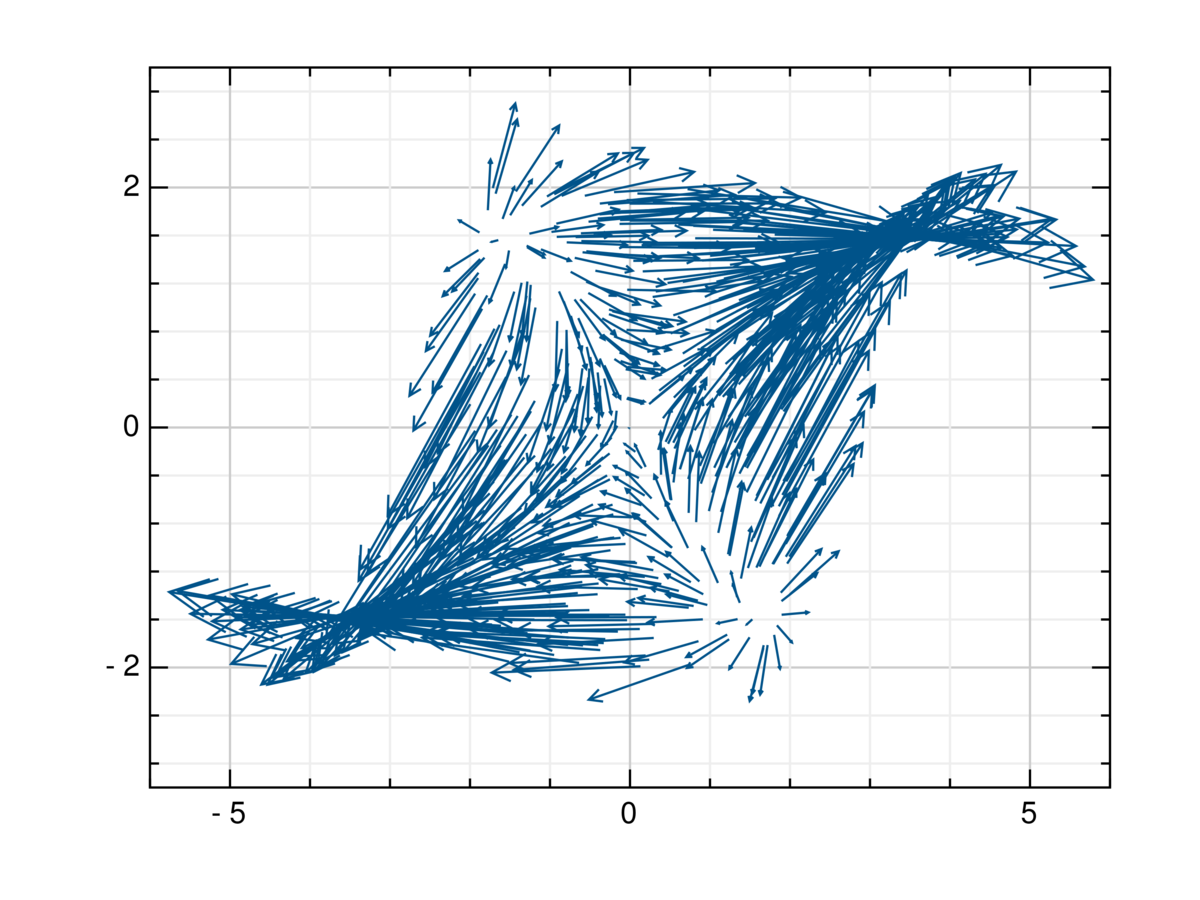

まぁよく学習できてそうである.