Python SVDによる低ランク近似
PythonでSVDで入力行列Aのランクをrankに落とすプログラム. ちなみに,C++バージョンはこっち.
import numpy as np import scipy as sp def SVD(A, rank): u, s, v = np.linalg.svd(A) ur = u[:, :rank] sr = np.matrix(sp.linalg.diagsvd(s[:rank], rank, rank)) vr = v[:rank, :] Rr = ur*sr*vr return Rr
ちなみにこのコードだと,O(n3)かかる.Arpack使うと,O(n2 r)でできるはず... scipy.sparse.linalg.svds を参考.(スパース行列じゃなくてもできる)
噂では,sklearn.decomposition.truncatedSVD も使えるようだ. 計算量をさらにO(n2 log r + r2 n)まで落とすこともできるようで,これはこちらの論文に載っている(らしい.私は読んでない)
SVDでrランク近似するの、普通にnumpy.linalg.svd使うとO(n^3)やん。
— ゆうだい.jl (@physics303) 2020年11月12日
でも噂では、O(n^2 r)でできるらしいじゃん。どうやるの?Juliaでも良い。既に実装されてるライブラリがあるはずだよね?#Julia言語
C++ eigenでランダム行列を作る
最小値LOから最大値HIの値を一様にとる連続分布で,N×Nの行列を作る方法.
#include <Eigen/Dense> #include <iostream> #include <cmath> using namespace Eigen; using namespace std; MatrixXd random_uniform_mtx(int N, double LO, double HI){ double range = HI - LO ; MatrixXd P = MatrixXd::Random(N, N); P = (P + MatrixXd::Constant(N, N, HI))*range/2; P = (P + MatrixXd::Constant(N, N, LO)); return P; }
Stack Overflow で見かけたコードだった気がするが,ぐぐっても見当たらなくなっていた...
C++で行列のランクを求める
あんまり良い方法が思い浮かばないので,いつもこんな風にやっているのですが,何か良いアイディアがあれば教えてください.
#include <Eigen/Dense> #include <iostream> #include <cmath> using namespace Eigen; using namespace std; int matrix_rank(MatrixXd mtx){ FullPivLU<MatrixXd> lu_decomp(mtx); auto rank = lu_decomp.rank(); return rank; }
C++ SVDによる低ランク近似
O(n3)で入力行列Pのランクをrにするアルゴリズムです.eigenをつかっています.
#include <iostream> #include <Eigen/Dense> #include <vector> #include <cmath> #include <time.h> #include <cstdio> #include <fstream> #include "utils.h" using namespace std; using namespace Eigen; MatrixXd SVD(MatrixXd& P, int r){ int const N = P.rows(); int const rank = r; //JacobiSVD<MatrixXd> svd(P, ComputeFullU | ComputeFullV); BDCSVD<MatrixXd> svd(P, ComputeFullU | ComputeFullV); MatrixXd SVD_P(N,N); MatrixXd U(N,N), Ur(N,rank-1); MatrixXd V(N,N), Vr(N,rank-1); MatrixXd S(N,N), Sr(rank-1, rank-1); VectorXd sigma(N); U = svd.matrixU(); V = svd.matrixV(); sigma = svd.singularValues(); S = sigma.array().matrix().asDiagonal(); Ur = U(all, seq(0,rank-1)); Vr = V(all, seq(0,rank-1)); Sr = S(seq(0,rank-1),seq(0,rank-1)); SVD_P = Ur * Sr * Vr.transpose(); return SVD_P; }
Julia言語 Sinkhorn Knopp アルゴリズムを実装した.
先日の記事のコードをJulia化した.
using LinearAlgebra function quick_convergence_check(v, v_new, u, u_new, eps) if norm( abs.(v - v_new) ) < eps if norm( abs.(u - u_new) ) < eps return true end end return false end function main(A, r, c ; eps = 1.0E-7) r = vec(r) c = vec(c) # vector r and c should be normalized. rs = sum(r) cs = sum(c) r = r / sum(r) c = c / sum(c) # Initial Step v = copy(r) u = copy(c) cnt = 0 while true # Sinkhorn-knopp Step v_new = r ./ ( A' * u ) u_new = c ./ ( A * v_new ) if quick_convergence_check(v, v_new, u, u_new, eps) break end # Initial Step if cnt > 25000 println("calculation did not converge") exit() end v = v_new u = u_new cnt += 1 end P = diagm( vec(u) ) * A * diagm( vec( v )) return P end A = [1 5 3 6; 9 5 5 6; 1 7 10 9; 2 3 1 4] r = [7 7 4 2] c = [1 2 3 4] P = main(A,r,c) display(P) println("\n", sum(P,dims=1) ) println("\n", sum(P,dims=2) )
Python Sinkhorn Knopp アルゴリズムを実装した.
非負行列の行和,列和を揃える操作を行うSinkhorn Knoppアルゴリズムをpythonで実装しました.Julia版はこっち. 入力行列Aのi行目の行和がr[i], j列目の列和がc[j]になるようにするアルゴリズムが以下です.
Sinkhorn Knoppアルゴリズムは,エントロピー拘束付き最適化と関りがあります. 最適輸送の文脈での最重要アルゴリズムの1つです.
import numpy as np def main(A, r, c, eps = 1.0E-7): """ Input : Matrix A, vectors r and c A can be a rectangular matrix Output : P = diag(u) A diag(v) Sum_i p_1i = c_i / sum(c) Sum_j p_j1 = r_j / sum(r) <=> sum(P.T) = c sum(P) = r """ assert A.ndim == 2, "A is not matrix" assert r.ndim == 1 and c.ndim == 1, "r and c should be vectors." assert A.shape[0] == c.shape[0], "dim of A does not correspond to r ones." assert A.shape[1] == r.shape[0], "dim of A does not correspond to c ones." # vector r and c should be normalized. r = r / np.sum(r) c = c / np.sum(c) # Initial Step v = np.copy(r) # same as v = r / ( A.T @ c) u = np.copy(c) # same as u = c / ( A @ v) cnt = 0 while True: # Sinkhorn-knopp Step v_new = r / ( A.T @ u) u_new = c / ( A @ v_new) if quick_convergence_check(v, v_new, u, u_new, eps) == True: break if cnt > 25000: print("calculation did not converg") exit() v = v_new u = u_new cnt += 1 P = np.diag(u) @ A @ np.diag(v) return P def quick_convergence_check(v, v_new, u, u_new, eps): if np.linalg.norm(abs(v - v_new)) < eps: if np.linalg.norm(abs(u - u_new)) < eps: return True return False if __name__ == "__main__": A = np.array([[1,5,3,6],[9,5,5,6],[1,7,10,9],[2,3,1,4]], dtype = "float64") c = np.array([7,7,4,2], dtype="float64") r = np.array([1,2,3,4], dtype="float64") P = main(A, r, c) print(sum(P.T)) print(sum(P))
ちなみに,rとcを全て1からなる行列にすると求まる行列は二重確率行列と呼ばれるのですが,二重確率行列のいろいろな性質についてはこの論文が参考になります.
Julia言語 行列の一部を削除する.
また強いツイッタラーに教えてもらった.
n×n行列のs行目とt列目を削除して,(n-1)×(n-1)行列を得たい,みたいなときに便利なのがInvertedIndices
行列aの取り除きたい列をs,取り除きたい行をtとすると,a[Not(s), Not(t)] で所望の行列を得る.
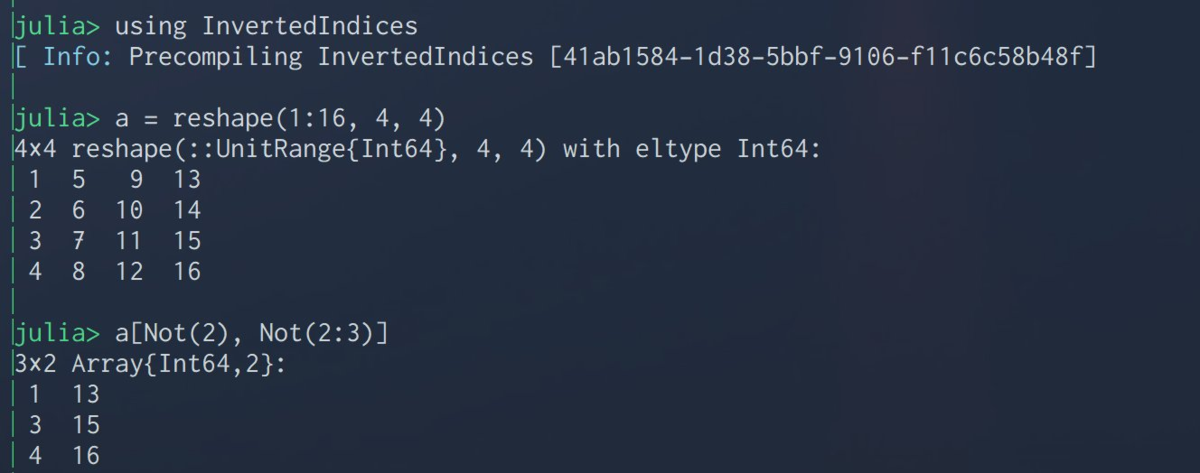
こちらのツイートもかなり参考になります.A[begin:end .≠s , begin:end .≠t]でもできる模様
#Julia言語 おお!https://t.co/4VGQZ9EfRN はシンプルでよくできていますね!(添付画像3)
— 黒木玄 Gen Kuroki (@genkuroki) 2020年12月1日
これに頼らない方法としては、
X[begin:end .≠ 2, begin:end .≠ 2]
があります。詳しくはhttps://t.co/pulsHtUBVA
もしくは添付画像を参照。参考になりそうな書き方をしています。 pic.twitter.com/jaCuA0w2Cs
Julia言語 非負値行列因子分解
ここにある更新式を見て,実装した.白抜きの丸はelement-wiseの積だと理解した.
https://www.jjburred.com/research/pdf/jjburred_nmf_updates.pdf
収束判定条件はsklearnのNMFの標準設定とできるだけ揃えた.
scikit-learn.org
以下実装.
using LinearAlgebra using Random Random.seed!(123) function KL(A, B) n, m = size(A) kl = 0.0 for i = 1:n for j = 1:m kl += A[i,j] * log( A[i,j] / B[i,j] ) - A[i,j] + B[i,j] end end return kl end function nmf_euc(X, r ; max_iter=200, tol = 0.0001) m, n = size(X) W = rand(m, r) H = rand(r, n) error_at_init = norm(X - W*H) previous_error = error_at_init for iter in 1:max_iter H .= H .* ( W' * X ) ./ ( W' * W * H ) W .= W .* ( X * H') ./ ( W * H * H' ) if tol > 0 && iter % 10 == 0 error = norm(X - W*H) if (previous_error - error) / error_at_init < tol break end previous_error = error end end return W, H end function nmf_kl(X, r ; max_iter=200, tol = 0.0001) m, n = size(X) W = rand(m, r) H = rand(r, n) one_mn = ones(m, n) error_at_init = KL(X, W*H) previous_error = error_at_init for iter in 1:max_iter println(KL(X, W*H)) H .= H .* ( W' * ( X ./ (W*H))) ./ ( W' * one_mn ) W .= W .* ( (X ./ (W*H) ) * H') ./ ( one_mn * H' ) if tol > 0 && iter % 10 == 0 error = KL(X, W*H) if (previous_error - error) / error_at_init < tol break end previous_error = error end end return W, H end
更新するところ,H = hogehoge より,H.= hogehoge の方が微妙に速いって強いツイッタラーに教えてもらった.
Performance Tips · The Julia Language
ちなみに,sklearnでKL-NMFはこんな感じ.デフォルトのsklearnの設定より,上のJulia実装の方が,コスト関数を小さくできる(なぜ?)
import numpy as np from math import log from sklearn.decomposition import NMF rank = 3 nmf = NMF(rank, beta_loss='kullback-leibler', alpha=0, verbose=1,solver='mu') # NMF W = nmf.fit_transform(X) H = nmf.components_ X_nmf = np.dot(W, H)
追記
αダイバージェンスでNMFできるように拡張した.
genkaiphd.hatenablog.com
Surface Pro 7 / Bluetoothを ON にすると任意の操作がぐらつく.
朝起きて,珈琲飲んで,Surface を見ると電源が切れている(普段はスリープモード).
変だなと思い,Surfaceを立ち上げてみると,マウス操作のラグがすごい.タッチパネルもすごいラグ.3回再起動したけど治らず.ブルートゥースを切ると症状なくなる.ブルートゥースをON/OFF繰り返しても治らない.
少し怖いけど,
Bluetoothとその他のデバイス→その他のBluetoothオプション→ハードウェア→Bluetooth Device→プロパティ→ドライバ→デバイスのアンインストール
を実行.次にIntelのサイトからBluetoothドライバをインストールして再起動.
これで症状は治った.原因は不明.
Julia言語 Plotsの軸が見切れる問題
JuliaのPlotsとてもカッコ良いのですが,このように軸が見切れたりします.
そういうときはusing Plots.PlotMeasuresしたあとに,
plot(x,y, bottom_margin = 20mm )
のように,marginオプションを使えば解決できる.
left_margin, bottom_margin, right_margin, top_margin など同様に使える.というか単位に"mm"をつけるの,Juliaっぽくていいな.
Julia言語 stringをfloatにする.
x = 3 ; x = float(x) でint型をfloatに変換できますが,x = "3.0" みたいなstring を float(x)としてもうまく変換できません.そういう時は,parse()を使います.
parse(Float64, x)
で無事にstringをFloat64にできます.
Julia言語 コンソールに表を表示させる.
コンソール上にいい感じに数値を並べていくには,以下URLにあるような
Using StringLiterals するのがよさげ.
ただ,インストールに手間取った. Pkg.clone()はどうも過去の遺物っぽくて,
pkg > add "https://github.com/JuliaString/StringLiterals.jl"
でインストールできた.
Julia言語 行列にmissingを代入する.
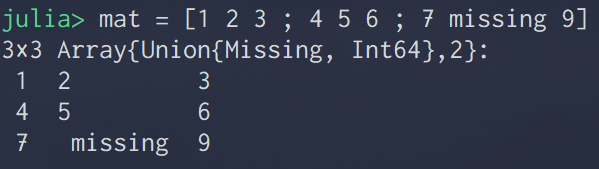
Juliaには欠損値の型 missing がある.
欠損値を含む行列を次のように定義できる
じゃあ今度は既存の行列の一部を欠損にできるかやってみようとするうまくいかない.
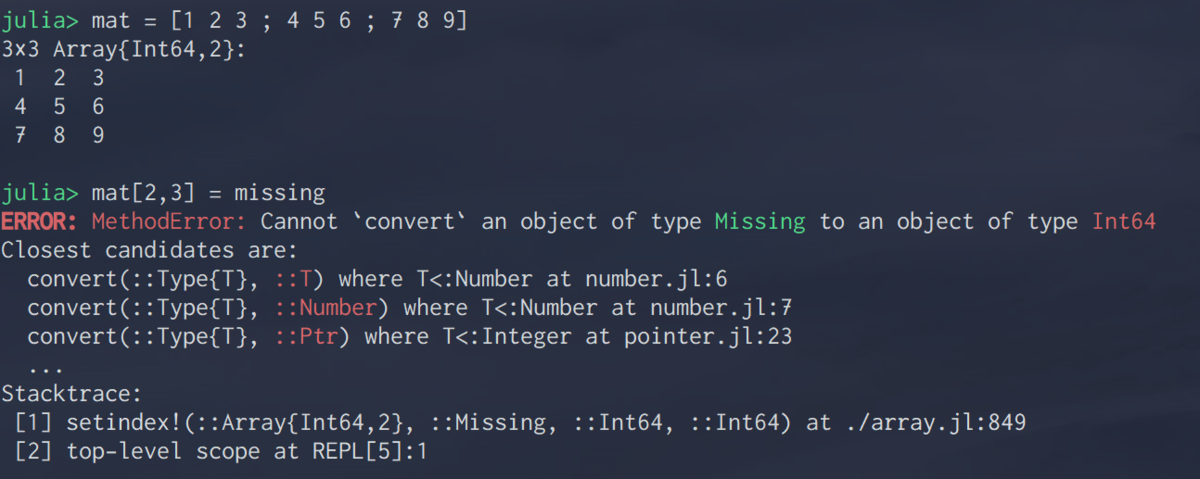
ぐぐると,dfを使った解決策とかがでてくる.DataFrame使いたくない...
この問題は,missingを含みうる型で行列を定義することで解決する.
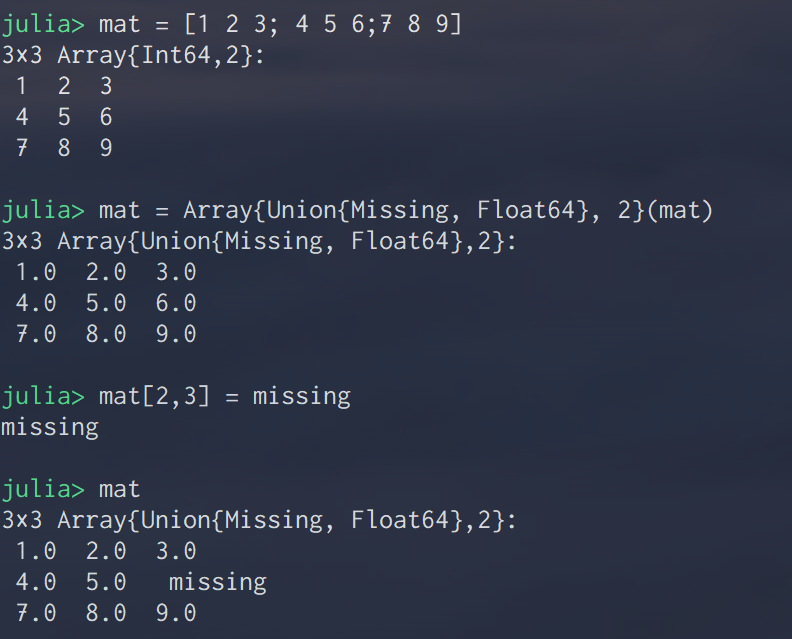
このように定義された行列はmissingもFloat値も代入できる. missingもfloat64のどちらも値として持てるn×n行列は次のように初期化する.
mat = Array{Union{Missing, Float64}, 2}(undef,3,3)