まぃふぇいばりっと

機械学習やってます．Julia大好きです．勉強したことの殴り書きです．

Julia言語でランダムウォーク

Julia言語 書評 確率統計

小針先生の確率統計の本を読んだ．教訓がたくさん詰まった本当に良い本だったと思う．６章の「酔歩」がとても印象に残っている．独立した章なので，確率の基本的なことが分かっていれば読める．

時刻t=0で原点に居る酔っ払いが，確率1/2で西へ，確率1/2で東に一歩進むランダムウォークを考えると，原点付近をうろちょろしそうだけど，まぁ，冷静に考えればそんなことはない．Juliaで酔っぱらいを召喚して，実験してみる．

function random_walker(n_steps)
    traj = [0]
    for step = 1 : n_steps
        coin = rand()
        pos = traj[step]
        if coin > 0.5
            append!(traj, pos + 1)
        else
            append!(traj, pos - 1)
        end
        println("step: $step pos: $pos")
    end
    return traj
end

trajに各ステップでの酔っぱらいの位置が保存される．とりあえず酔っぱらいを5人くらい召喚しよう．

using Plots
function main(n_walkers)
    n_steps = 30000

    fnt = font(16, "times")
    p_r = plot(legend = :topleft)
    for walker = 1:n_walkers
        traj = random_walker(n_steps)
        plot!(p_r, [1:n_steps+1;], traj,
            xlabel      = "step",
            ylabel      = "pos",
            xguidefont  = fnt,
            yguidefont  = fnt,
            xtickfont   = fnt,
            ytickfont   = fnt,
            titlefont   = fnt,
            title       = "trajectory of radom walkers",
            size        = (1200, 600),
            linewidth   = 3,
            label       = "random_walker $walker")
    end
    plot!([0.0], st=:hline, label=false)
    savefig(p_r, "traj_rw.png")
end

main(5)

これをプロットしてみる．横軸がステップ数，縦軸が酔っぱらいの位置である．

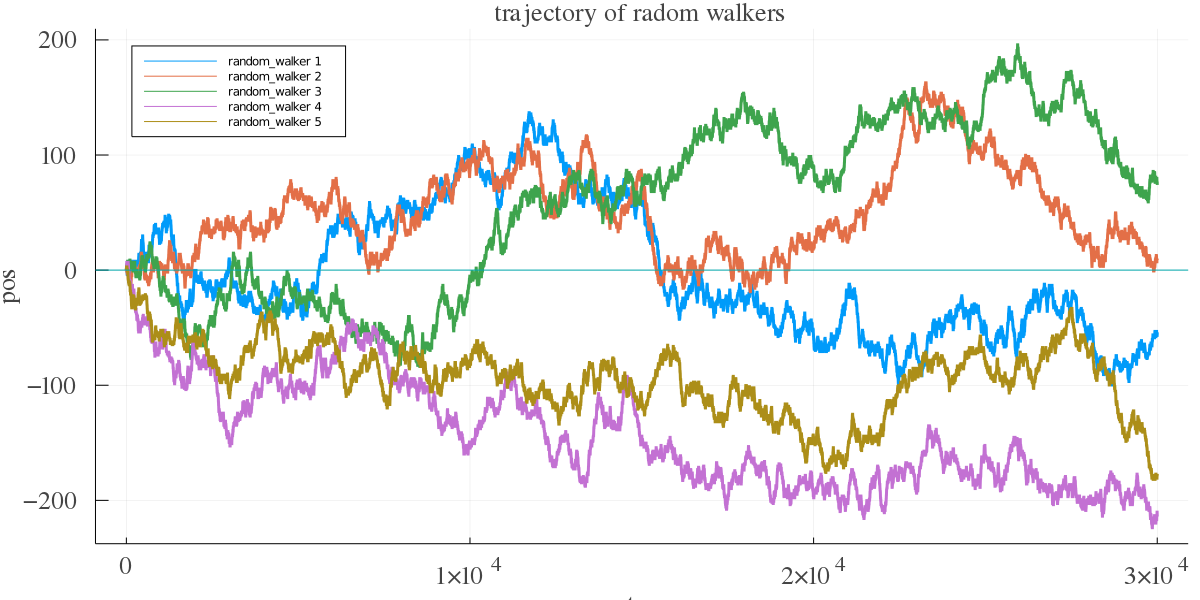
f:id:physics303:20210104141952p:plain

観ての通り，原点付近をうろちょろしているわけじゃない．実は，単位時間あたりに原点より東に居る時間をx，西に居る時間を1-xとすると，この分布は

p(x) = (π√(x(1-x)))-1

になって，東か西かのどちらか片方ばかりに多くいる確率の方が大きい．

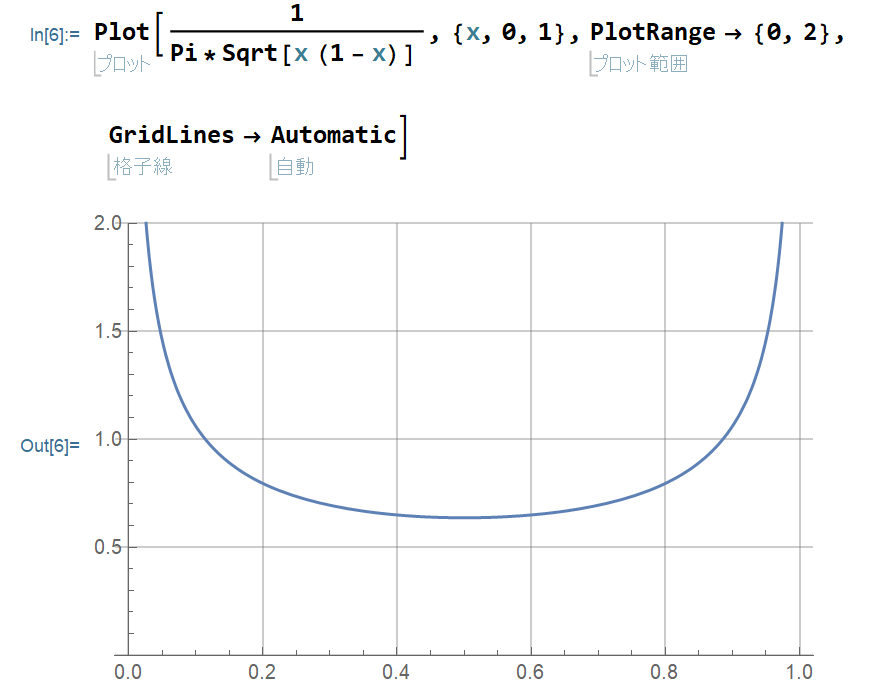
f:id:physics303:20210104142100p:plain

また，どんなに長い時間観測しても，「１度も原点に戻らない」確率と「１度しか原点に戻らない」確率が最も大きく，m回復帰する確率は，mが大きいほど小さいことが示せる．この話は，小針先生の「確率・統計入門」の第6章「酔歩」に証明を含め詳しく議論されてる．古い本だけど，とても読みやすい．独特の言い回しで著者の息遣いが聞こえてくるすごい良い本だと思う．例えば，このランダムウォークに関して小針先生は

正の領域に居る時は善行，負の領域に居る時は悪行を行っている時間とすると，善悪半々というマジメ人間は最も少く，悪い奴ほどはびこり，あるいは善人ほど多いということなのである．これは真実かもしれない p148

とか，

原点のまわりをウロウロするという最初の予想に反して，それほどセンチメンタルに故郷を慕うのではない p154

とかしゃれたことを言うのである．楽しい．

特に最初の第一章は「円に任意の弦をひくとき，その長さが内接正三角形の一片より長くなる確率を求めよ」という例題に対してA君B君C君の異なる回答の総括として，

真理というものがどこかにあって、それを探究するのが学問、ではなくて、何を仮定すれば何が結論されるかの論理の連鎖が学問である。

と言っていて，読んでて興奮するものがある．

どうやら小針先生はこの本を完成させることなく急逝し，旧友たちがこの本を完成させたようである．この本の前書きやあとがきには，なかなかドラマを感じるので，本屋で見かけたらぜひ手に取ってみたらどうだろう．

全然関係ないけど，酔歩つながりで，「酔歩する男」っていう物語がある．玩具修理者に収録されている．これがなかなか鳥肌の立つよいタイムリープ系SFで面白いのです．

Julia言語 αダイバージェンスで非負値行列因子分解

機械学習 線形代数 Julia言語 論文実装 行列分解

こないだのJuliaでNMFしたコードを一般のαダイバージェンスの尺度でNMFできるようにしました． αダイバージェンスの定義はここを参考にしました． 更新式はこの論文の2節に書いてあります．なんと更新式の一部をα倍したり1/α倍したりするだけ，簡単！

using LinearAlgebra
using Random
Random.seed!(123)

function D_KL(A, B)
    n, m = size(A)
    kl = 0.0
    for i = 1:n
        for j = 1:n
            kl += A[i,j] * log( A[i,j] / B[i,j] ) - A[i,j] + B[i,j]
        end
    end
    return kl
end

function D_alpha(A, B, alpha)
    # D_alpha(A, B, 1) = D_KL(A, B)
    # D_alpha(A, B, 0) = D_KL(B, A)
    if alpha == 1
        return D_KL(A, B)
    end
    if alpha == 0
        return D_KL(B, A)
    end

    A = A / sum(A)
    B = B / sum(B)

    n, m = size(A)
    d_alpha = 0.0
    for i = 1:n
        for j = 1:m
            d_alpha += alpha * A[i,j] + (1-alpha) * B[i,j] - X[i,j].^alpha * B[i,j].^(1-alpha)
        end
    end
    return 1.0 / ( alpha - alpha^2 ) * d_alpha
end

function nmf_alpha(X, r, alpha; max_iter=200, tol = 0.000001)
    m, n = size(X)
    W = rand(m, r)
    H = rand(r, n)
    one_mn = ones(m, n)

    error_at_init = D_alpha(X, W*H, alpha)
    previous_error = error_at_init
    for iter in 1:max_iter
        H .=  H .*( ( W' * ( X ./ (W*H) ).^alpha) ./ ( W' * one_mn )).^(1.0/alpha)
        W .=  W .*( ( ( X ./ (W*H) ).^alpha * H') ./ ( one_mn * H' )).^(1.0/alpha)

        if tol > 0 && iter % 10 == 0
            error = D_alpha(X, W*H, alpha)
            if (previous_error - error) / error_at_init < tol
                break
            end
            previous_error = error
        end
    end

    return W, H
end

こーゆのってどうやってテストすればいいんでしょうね． sklearnにはαダイバージェンスでNMFは実装されてないみたいなので結果を比較できなかった．更新式の一部をα倍するだけなので，pythonでも比較的容易に実装できると思う． そのうちついでにJuliaでβダイバージェンスでNMFも実装しておきたいな．

そろそろ研究で必要なので非負テンソル因子分解を実装しないといけない．．．

Julia言語 適当な分布に従うテンソルをつくる

Julia言語

各要素が適当な分布に従うテンソルをつくる．例えば，中心がmu, 分散がsigmaの一次元ガウス分布に各要素が従うD×M×Nテンソルをつくりたければ

using Distributions

mu = 0
sigma = 5
D = 2
M = 3
N = 5
dist = Normal(mu, sigma)
X = rand( dist, (D, M, N) )

とすればいい．

Julia言語 手っ取り早く B = { b ∈ {±1}^N } を生成する方法

Julia言語

集合 B ={ b ∈ {±1}^N } を得たい！ 僕が考えたのはこんな感じ．

using Combinatorics

function main(N)
    B=[]
    for n=1:N
        combs = collect(combinations(1:N,n))
        for comb in combs
            b = ones(N)
            for com in comb
                b[com] = -1
            end
            push!(B,b)
        end
    end
    return B
end

B = main(5)

display(B)

これを実行すれば

 [1.0, 1.0, 1.0, 1.0, 1.0]
 [-1.0, 1.0, 1.0, 1.0, 1.0]
 [1.0, -1.0, 1.0, 1.0, 1.0]
 [1.0, 1.0, -1.0, 1.0, 1.0]
 [1.0, 1.0, 1.0, -1.0, 1.0]
 [1.0, 1.0, 1.0, 1.0, -1.0]
 [-1.0, -1.0, 1.0, 1.0, 1.0]
 [-1.0, 1.0, -1.0, 1.0, 1.0]
 [-1.0, 1.0, 1.0, -1.0, 1.0]
 [-1.0, 1.0, 1.0, 1.0, -1.0]
 [1.0, -1.0, -1.0, 1.0, 1.0]
 [1.0, -1.0, 1.0, -1.0, 1.0]
 [1.0, -1.0, 1.0, 1.0, -1.0]
 [1.0, 1.0, -1.0, -1.0, 1.0]
 [1.0, 1.0, -1.0, 1.0, -1.0]
 [1.0, 1.0, 1.0, -1.0, -1.0]
 [-1.0, -1.0, -1.0, 1.0, 1.0]
 [-1.0, -1.0, 1.0, -1.0, 1.0]
 [-1.0, -1.0, 1.0, 1.0, -1.0]
 [-1.0, 1.0, -1.0, -1.0, 1.0]
 [-1.0, 1.0, -1.0, 1.0, -1.0]
 [-1.0, 1.0, 1.0, -1.0, -1.0]
 [1.0, -1.0, -1.0, -1.0, 1.0]
 [1.0, -1.0, -1.0, 1.0, -1.0]
 [1.0, -1.0, 1.0, -1.0, -1.0]
 [1.0, 1.0, -1.0, -1.0, -1.0]
 [-1.0, -1.0, -1.0, -1.0, 1.0]
 [-1.0, -1.0, -1.0, 1.0, -1.0]
 [-1.0, -1.0, 1.0, -1.0, -1.0]
 [-1.0, 1.0, -1.0, -1.0, -1.0]
 [1.0, -1.0, -1.0, -1.0, -1.0]
 [-1.0, -1.0, -1.0, -1.0, -1.0]

となって，所望の集合Bを得る．

これで，めでたしめでたしなのだが，もっと良い方法を強い人に教えてもらった．

a = [-1, 1]
B = vec(collect(Iterators.product(fill(a,4)...)))

これでも同じものが手に入る．Iteratorsを使いこなせるようになりたい．

また，他の強い人に，bit探索のノリでいけるんじゃないの？というコメントを貰いました．

for i in 0:2^N-1
    ptn = digits(i, base=2, pad=N)
    println(ptn)
end

所望のBにしたかったら，2倍して，1を引けばよい．これ，とても速い気がするんだけど，どうなんだろう．

そんなことせずに，無名関数でどうにかなることを知りました．

arr = [-1,1]
for i in 0:2^N-1
    ptn = digits(i, base=2, pad=N)
    println( (d -> arr[d+1]).(ptn) )
end

また，他の強い人によると，このように１行で済ませることもできるみたいです．

[[(-1)^parse(Int,string(i, base=2,pad=5)[k]) for k=1:5] for i=0:2^5-1 ]

また，他の強い人によると，map関数をうまく使えばもっとスマートのようです．

[map(x->2x-1, digits(i,base=2,pad=N)) for i in 0:2^(N)-1]

また，他の強い人によると，このようにもできるみたいです．

n = 4
[[(-1)^(i >> k & 1) for k in 0:n-1 ] for i in 1:2^n]

無料で観れる数理情報系の講義（自分用まとめ）

自分が勉強するのに役に立ったYoutubeで公開されている講義をどんどん追加していきます．

数学

松本多様体の内容を（かなり端折りながらも）丁寧に追っていく授業です．理解が深まりました．面白かった．

確率過程論を測度論、積分論を前提にせずに授業してくれているありがたい授業．

まだ観てないが，代数についての講義っぽい．

まだ観てないが，代数についての講義っぽい．ガロア理論に追いつくには良いかも？

計算機科学

物性物理学

修士課程の時に何度も繰り返しみた講義です．ベリー位相や物性のトポロジカルな性質などが非常に良くまとまっています．私が修士の時は，この辺りは優れた日本語の教科書がなかったので，この講義にはかなり助けられました．

Youtuber

Juliaでwandbを使ってみた．

Julia言語 機械学習

ひとまずpythonにwandbをインストールする．

pip install wandb

次に，JuliaにPyCallをインストールする．

(@v1.5) pkg> add PyCall

wandbの公式ページでアカウントをつくる．適当なプロジェクトを作る． その語，Pythonでwandbを使うようにjuliaで

julia > using PyCall
julia > wandb=pyimport("wandb")
julia > wandb.init(project="（プロジェクト名)")
julia > wandb.log( PyDict( 'epoch'=>1, 'loss'=>2) )
julia > wandb.log( PyDict( 'epoch'=>2, 'loss'=>3) )
julia > wandb.log( PyDict( 'epoch'=>3, 'loss'=>4) )

juliaを終了すると，logがアップロードされる模様．ブラウザでマイページを見てみると更新されているのが分かる．

Julia言語 経過時間を計測して，変数に代入

Julia言語

@time とかいろいろあるみたいですが，私が好きなのはこの方法

using BenchmarkTools

runtime = @elapsed begin
        (処理)
    end

これで変数runtimeに(処理)が終わるまでに要する時間が秒で代入されます．

追記

強い人に教わったのですが

result, runtime = @timed hoge()

でもいけそう．resultがhoge()の返り値，runtimeが経過時間

Julia言語 ST-HOSVDによる低ランク近似

Julia言語 線形代数 機械学習 行列分解

このスライドのp26, アルゴリズム2をJulia言語で実装しました．

https://mycourses.aalto.fi/pluginfile.php/1249889/mod_resource/content/1/Lecture6.pdf

素朴なHOSVDや，T-HOSVDより効率よく低ランク近似が実現できているらしいです． ArpackだとフルHOSVDができないので場合分けするのが悔しい...．（そもそもArpackは疎行列を念頭に置いたライブラリっぽい．）

using TensorToolbox
using LinearAlgebra
using Arpack

function STHOSVD(T, reqrank)
    N = ndims(T)
    tensor_shape = size(T)
    for i = 1 : N
        T_i = tenmat(T, i)
        if reqrank[i] == tensor_shape[i]
            USV = svd(T_i)
        else
            USV = svds(T_i; nsv=reqrank[i] )[1]
        end
        T = ttm( T, USV.U * USV.U', i)
    end

    return T
end

この文献のアルゴリズム1なども参考．

https://epubs.siam.org/doi/pdf/10.1137/110836067?casa_token=T3KIsgIjhgYAAAAA:HIUFLqzIk2SxvpmYfAsJUP_vovr7tHjvXw8BJxSpMG3PTOOjcirq3TeFv3YqpyI4xsRt5LzPxtEhiQ

Julia言語 Truncated HOSVDによる1ランク近似

Julia言語 機械学習

Julia言語で，T-HOSVDによりテンソルランクを１にするアルゴリズムを実装しました． この論文のアルゴリズム3を実装しました．

using TensorToolbox
using LinearAlgebra
using Arpack

function THOSVD(T)
    # Output is rank-1 tensor
    N = ndims(T)
    input_tensor_shape = size(T)

    u = []
    for n=1:N
        # Matricization of tensor by mode n
        Tn = tenmat(T,n)
        # First left singula vector of Tn
        un = svds( Tn ; nsv=1 ).U[:, 1]
        push!(u, un)
    end

    U = ttt(u[1],u[2])
    for n=3:N
        U = ttt(U, u[n])
    end

    println(size(U))
    lammda = innerprod(T, U)
    X = lammda .* U
    return X
end

T = [  1 -1   0 1 3 im 0 1 ;
         0.0  1 -im 1 1  0 2 -2im]
T = matten(T, 1, [2,2,2,2])
X_THOSVD = THOSVD(T)

Julia言語 SVDによる低ランク近似

Julia言語 機械学習

Julia でSVD をするときに，Lapackを使って

using LinearAlgebra

n = 10
A = rand(n, n)
svd(A)

としても良いのですが，これだとO(n3)必要ですね． ランクをrにするのに，完全なSVDをする必要はありません．Arpackのsvdsを使うべし．

using Arpack

n = 10
r = 5
A = rand(n, n)
svd = svds(A ; nsv=r, ritzvec=true)[1]
Ar = svd.U * diagm(svd.S) * svd.Vt

で10×10行列Aの5ランク近似がO(n2 r)で手に入ります．

julialinearalgebra.github.io

実際に時間はかってみるとこんな感じ． Arpackのほうがだいぶはやいが，rが大きいときは，Lapackの方がはやいっぽい．

using LinearAlgebra
using Arpack

n = 2000
A = rand(n, n)
@time svd(A);
# 4.236471 seconds (12 allocations: 183.350 MiB, 3.53% gc time)

r = 5
@time svds(A ; nsv=r, ritzvec=true)[1];
# 0.479803 seconds (1.35 k allocations: 840.125 KiB)

r = 10
@time svds(A ; nsv=r, ritzvec=true)[1];
# 0.654874 seconds (1.78 k allocations: 1.237 MiB)

r = 100
@time svds(A ; nsv=r, ritzvec=true)[1];
# 1.538005 seconds (3.57 k allocations: 11.446 MiB)

r = 200
@time svds(A ; nsv=r, ritzvec=true)[1];
# 2.692379 seconds (5.21 k allocations: 23.644 MiB)

r = 400
@time svds(A ; nsv=r, ritzvec=true)[1];
# 5.119713 seconds (7.29 k allocations: 50.736 MiB)

関連記事

Python SVDによる低ランク近似

C++ SVDによる低ランク近似

Julia言語 HOSVDによるタッカー低ランク近似

Julia言語 機械学習 線形代数

行列の低ランク近似がSVDによって実現されるように，テンソルの低（タッカー）ランク近似がHOSVDで実現できます．

なお，Eckart Youngの定理より，SVDがフロベニウスノルムの意味で最良低ランク近似を実現しますが，テンソルの場合はそのような保証はないと思います．

テンソルにおいては，タッカーランクとCPランクという異なるランクの定義が存在します．（以下，研究室のセミナーで用いた資料.間違ってたらゴメン）

f:id:physics303:20201210212407p:plain

f:id:physics303:20201210212511p:plain

記号×_nはモードn積です．モード積の定義はこちらを参考にすると良いと思います．

juliaでHOSVDがさくっとできないかいろいろ試してましたが，TensorToolboxを使うのが手っ取り早そうですね．例として3×3×3テンソルTをHOSVDによってタッカーランク(2,2,2)で近似するJuliaコードは以下．

using TensorToolbox

function HOSVD(T, reqrank)
    X = hosvd(T, reqrank=reqrank)
    g = X.cten
    Us = X.fmat

    #X = ttm(g, [Us[1],Us[2],Us[3]],[1,2,3])
    X = ttm(g, [Us...])
    return X
end

T = rand(3,3,3)
println("input tensor")
display(T)

X = HOSVD(T, [2,2,2])
println("\n\noutput tensor")
display(X)

println("\n\nerror")
println(norm(X-T))

タッカーランクを[3,3,3]にすると，エラーが0になります．

X.cten でコアテンソルが取り出せて，X.fmat でスライドでいうところのU_1,U_2,…を取り出しています． ttmの使い方はgithubに丁寧に載ってます．ttm(X, A, 2)がXとAのモード2積 X ×_2 A です．

github.com

ところで，この実装って Truncated HOSVD になっているのだろうか．．．

Julia言語 n階のテンソルを初期化する．

Julia言語

3×3×3のテンソルを用意したいときは，X = rand(3,3,3) みたいにするとおもいますが，階数が大きい時に X = rand(i1,i2,i3,i4, ..., ,in って手動で入力するのが大変だったので，i = [i1,i2,i3,…,in] を用意して

using TensorToolbox
X = diagt(i)

みたくしてたけど，どうもX = rand(i...) で良いらしい．... は splat演算子というらしく，ドキュメントにもちゃんと記述がある． docs.julialang.org

n階のテンソルの初式化をするなら， X = Array{Float64, n}(undef, i...) のようにすればよいね．