Julia言語 L1ノルムでのテンソルランク１近似の解析解

3階のテンソルをL1ノルムの尺度で近似するランク１テンソルを見つけます，という論文を実装した．論文のタイトルにexact solutionがあるけど，L1ノルムの意味での最良１ランク近似をしてるわけではないので注意（かなり混乱した）．

arxiv.org

最近，L1が流行っているのかな．著者にお願いしてuploadしてもらったpythonコードとまったく同じ結果を返したので，このjulia実装は正しいと思う．私はgreedyのバージョンしか実装していないので，もっと速くする方法も論文を読めば載ってます（実装大変そうだからあきらめたけど，pythonコードを翻訳すればいけるかも？）

github.com

using TensorToolbox
using LinearAlgebra
using Arpack

function exactL1(tensor)
    X = tenmat(tensor, 1) #mode-1 matricization
    (D, M, N) = size(tensor)
    B = vec(collect(Iterators.product(fill([-1,1],N)...)))
    numOfCandidates = 2^N

    metopt = 0
    bopt = undef
    for n = 1:numOfCandidates
        b = collect(B[n])
        Z = X * kron(b, Matrix(I, M, M))
        sigmamax = svds(Z, nsv=1)[1].S[1]
        if sigmamax > metopt
            metopt = sigmamax
            bopt = b
        end
    end

    USV = svds( X*kron(bopt, Matrix(I,M,M)), nsv=1)[1]
    uopt = USV.U[:,1]
    vopt = USV.Vt[1,:]
    return uopt, vopt, bopt, metopt
end

入力行列の復元は原論文に従って，こんな感じ．試しにランク１テンソルを入力にしてみると，エラーがとても小さくなることが確かめられた．

P = [1 2]
Q = [2 3 4]
R = [4 5 6 7]
T = dropdims( ttt(ttt(P,Q),R) )
uopt,vopt,bopt,metopt = exactL1(T)

T1 = zeros(2,3,4)
for i = 1 : 4
    T1[:,:,i] = ( uopt * uopt' ) * T[:, :, i] * ( vopt * vopt' )
end

println( norm(T-T1) )

C++ 行列バランシング

行列バランシングと言えば，sinkhornですが，今回はこの論文を実装しました．

arxiv.org

（論文では自然勾配法使ってますが，ここでは，１次までしか実装してないです）

#include <iostream>
#include <Eigen/Dense>
#include <vector>
#include <cmath>
#include <time.h>
#include <cstdio>
#include <fstream>

using namespace std;
using namespace Eigen;

MatrixXd balance(MatrixXd& P, double lr){
    int N = P.rows();
    MatrixXd eta(N, N), theta(N, N);
    VectorXd eta_beta(N);

    // get eta_beta;
    for (int i = 0; i < N ; i++){
        eta_beta( i ) = ( 1.0 * N - 1.0 * i ) / (1.0 * N);
    }

    // get theta of input
    // we need all element to update p in iteration.
    double sum;
    for (int i = 0; i < N; i++){
        for(int j = 0; j < N; j++){
            sum = 0.0;
            sum = log( P(i, j) );
            if (0 < i)
                sum -= log( P( i-1, j) );
            if (0 < j)
                sum -= log( P( i, j-1 ) );
            if (0 < i and 0 < j)
                sum += log( P( i-1, j-1) );
            theta(i, j) = sum;
        }
    }

    // get eta of input
    eta( 0, N - 1 ) = P.col( N - 1 ).sum();
    eta( N - 1, 0 ) = P.row( N - 1 ).sum();
    for (int i = 2; i < N; i++){
        eta( 0, N - i ) =  eta( 0, N - i + 1) + P.col( N - i ).sum();
        eta( N - i, 0 ) =  eta( N - i + 1,0 ) + P.row( N - i ).sum();
    }

    int cnt = 0;
    while(true){
        // e-projection
        for(int i = 0; i < N ; i++){
            theta(i, 0) -= lr * ( eta(i, 0) - eta_beta( i ) );
            theta(0, i) -= lr * ( eta(0, i) - eta_beta( i ) );
        }

        // update prob by theta
        double logp_ij;
        for (int i = 0; i < N; i++){
            for (int j = 0; j < N; j++){
                logp_ij = 0.0;
                logp_ij = theta(i, j);
                if ( 0 < i )
                    logp_ij += log( P(i-1, j) );
                if ( 0 < j )
                    logp_ij += log( P(i, j-1) );
                if ( 0 < j and 0 < i )
                    logp_ij -= log( P(i-1, j-1) );

                P(i, j) = exp( logp_ij );
            }
        }

        // normalize
        P = P / P.sum();

        // update eta by prob
        eta( 0, N - 1 ) = P.col( N - 1 ).sum();
        eta( N - 1, 0 ) = P.row( N - 1 ).sum();
        for (int i = 2; i < N; i++){
            eta( 0, N - i ) =  eta( 0, N - i + 1) + P.col( N - i ).sum();
            eta( N - i, 0 ) =  eta( N - i + 1,0 ) + P.row( N - i ).sum();
        }


        cnt += 1;
        if (cnt > 2000) break;
    }

    return P;
}

int main(){
    double LO = 0.0; // minimu value of element of random matrix;
    double HI = 1.0; // maximu value of element of random matrix;
    double range = HI - LO;
    double lr = 0.1;

    int N = 25; // matrix dimenstion
    MatrixXd Q(N, N);  // output matrix

    // producting random input matrix P
    MatrixXd P = MatrixXd::Random(N, N);
    P = (P + MatrixXd::Constant(N, N, 1.0))*range/2;
    P = (P + MatrixXd::Constant(N, N, LO));

    /*
    P <<1,5,3,6,
        9,5,5,6,
        1,7,10,9,
       2,3,1,4;
   */

    P = P / P.sum();
    cout << "input matrix" << endl << P << endl;
    Q = balance( P, lr );
    cout << "output matrix" << endl << Q << endl;

    double rowsum,colsum;
    for(int i=0;i<N;i++){
        colsum = Q.row(i).sum();
        rowsum = Q.col(i).sum();
        printf("%d colsum = %f \t rowsum = %f\n",i,colsum,rowsum);
    }

}

Julia言語 特定の文字が文字列に何回現れたか数える方法．

文字列hogehogeにhが何回出てくるか数えたい．ぐぐると

str = "hogehoge"
cnt = sum([1 for i = eachmatch(r"h", str)])

とかいいんじゃね？と書いてある．

強い人にはもっとシンプルに

sum(split(str, "").=="h")

で良いと教わった．なるほど．

追記

強い人に直訳を教わった．

count(==('h'), str)

Julia言語 高速3階テンソル1ランク近似手法SeROAPの実装

3階のテンソルTをST-HOSVD, T-HOSVDより正確に高速に１ランク近似できる手法をJulia言語で実装した． あ，ここでいう階っていうのは，rank(T)じゃなくて，ndims(T)ね．3-waysとか，3-orderってこと．日本では，ndimsを階っていうので，（CP）ランクと混ざって良く分からなくなる．この手法は3階テンソル以外にも使えるけど，ST-HOSVDやT-HOSVDより，より近似をする理論的保証があるのは3階のときのみ． ちょっとめんどくさかったので，入力行列Tの型をI1×I2×...×Inとしたとき，I1 >= I2 >= … を仮定している．

アルゴリズム詳細はこの論文のアルゴリズム2を参照．

arxiv.org

実装

using TensorToolbox
using LinearAlgebra
using Arpack
using TensorDecompositions

function SeROAP(T)
    # arxiv.org/pdf/1508.05273.pdf
    # input_tensor_shape = [I1, I2, ... , In]
    #  I1 >= I2 >= ... >= In have to be satisfied ?
    # input is any complex tensor
    # output is rank-1 complex tensor
    # cost function is L2
    # in case of 3-ways tensor, SeROAP is better than HOSVD

    N = ndims(T)
    input_tensor_shape = size(T)

    Vs = []
    vs = []
    V = tenmat(T,1)
    V0 = copy(V)
    for n=1:N-2
        push!(vs, svds( V ; nsv=1 )[1].V[:,1])
        push!(Vs, reshape(vs[n], input_tensor_shape[n+1], prod(input_tensor_shape[n+2:N])))
        V = Vs[n]
    end
    u = svds( V ; nsv=1 )[1].U[:, 1]
    v = svds( V ; nsv=1 )[1].V[:, 1]
    w = kron( conj(v), u)

    X_n = undef
    for n = N-2 : -1 : 1
        if n != 1
            X_n = ( Vs[n-1] * w ) * w'
        else
            X_n = ( V0 * w ) * w'
        end
        w = vec(X_n)
    end

    X = matten(X_n, 1, collect(input_tensor_shape) )
    return X
end

研究には使わないけど，一緒にDCPDを実装しておこうかな．

Julia言語 DataFrameの列の名前を変える．

ついにDataFrameに入門してしまった...． 途中で列の名前を変えるにはこうする．

using DataFrames

names = ["colname1", "colname2", "colname3"]

data = rand(3,3)
df  = DataFrame(data)
rename!(df, Symbol.(names))

Symbolに変えないといけないことに気が付かなくてだいぶはまってしまった... ちなみに，列の名前の一覧を取り出したかったら，propertynames(df)すればいい．

言わずもがな，はじめから

data = rand(3,3)
names = ["colname1", "colname2", "colname3"]
df = DataFrame(data, names)

とすれば所望のものは手に入る．

1から始める Juliaプログラミング を読んだ．

最近，毎日Juliaを書いているので，買って読んでみた．結論から言うと本当に良い買い物をしたと思う．

薄い技術書だけど、内容は評判通りかなり濃厚．Juliaの基本的な言語機能の他にも、コンパイラへのヒントの書き方、メモリ割り当てを削減するtips、プロファイリングの方法、ドキュメントやdocstringの書き方，CやPythonやRの呼び出し方まで触れてて本当に勉強になった。メタプログラミングという言葉も初めて知った。いままで謎だったマクロの正体が多分わかった。シンボルの説明が丁寧だった。型の理解がかなり整理された。(そういえばmissing型についての言及はないですね)．

役に立つ情報満載．もちろんこういう情報は全て公式ドキュメントに載っていると思うんだけど，あの公式ドキュメント全部に目を通すのは分量的にきついと思うので，この本を通して読んでみるといいと思う．

なお，この本の初めの方に「初めてプログラミングを学ぶ人でも読める」みたいなことが書いてあったけど，それは嘘だと思う．内容はかなり親切に分かりやすく説明されていて，Pythonを触ったことがあれば，概ね理解できるとは思うんだけど，少なくとも，自分がプログラミングをやったことなかった時にこれを読んで，理解できたかというと，そんなことはないと思う．

Julia言語 高速非負テンソル分解lraSNTDを実装した．

Sequential nonnegative Tucker decomposition based on low-rank approximation(lraSNTD) を実装した．アルゴリズムは原論文を参考にした．

www.semanticscholar.org

前回のlraNMFを活用して高速に非負タッカー分解をしようっていうノリ．

using TensorToolbox
using LinearAlgebra
using Arpack
using TensorDecompositions

function lranmf_mu(X, r ; max_iter=200, tol = 1.0E-3, verbose = false)
    # lranmf_mu is effective when r << min(n,m)
    # input is a nonnegative tensor
    # proposed by Guoxu Zhou in 2012
    # https://ieeexplore.ieee.org/document/6166354

    n, m = size(X)
    epsilon = 0.0001

    # See step1 in section II-B in the paper
    if r == min(n, m)
        svd_X = svd(X)
    else
        svd_X = svds(X; nsv=r, ritzvec=true)[1]
    end
    Achil = svd_X.U * diagm(svd_X.S)
    Bchil = svd_X.V

    # See step2 in section II-B in the paper
    A = rand(n, r)
    B = rand(m, r)
    cost_at_init = norm(X - A*B')
    previous_cost = cost_at_init
    for iter = 1:max_iter
        B .= B .* ( max.( Bchil*(Achil' * A), epsilon ) ) ./ ( B*(A'*A) )
        A .= A .* ( max.( Achil*(Bchil' * B), epsilon ) ) ./ ( A*(B'*B) )

        if tol > 0 && iter % 10 == 0
            cost = norm(X - A*B')
            if verbose
                println("iter: $iter cost: $cost")
            end
            if (previous_cost - cost) / cost_at_init < tol
                break
            end
            previous_cost = cost
        end
    end

    # A * B' is rank-r matrix
    return A, B'
end

function lraSNTD(Y, reqrank)
    # Sequential nonnegative Tucker based on lraNMF
    # input is a onnegative matrix
    # proposed by Guoxu Zhou in 2012
    # https://ieeexplore.ieee.org/document/6166354

    N = ndims(Y)
    input_tensor_shape = size(Y)

    # See section IV-2) in the paper
    # get non-negative factors
    A = []
    for n=1:N
        # Yn is Matricization of tensor Y by mode n
        Yn = tenmat(Y, n)
        An, _ = lranmf_mu(Yn, reqrank[n])
        push!(A, An)
        # ttm(Y,An,n) is mode-n product of tensor X and matrix An
        Y = ttm(Y, pinv(An), n)
    end

    # reproduce
    Y = ttm(Y, A[1], 1)
    for n=2:N
        Y = ttm(Y, A[n], n)
    end

    return Y
end

reqrankはベクトルをいれる．たとえば，10×10×10テンソルYをタッカーランク(3,3,3)にしたければ，

Y = rand(10,10,10)
T = lraSNTD(X, [3,3,3])

とすれば，タッカーランク(3,3,3)でYを近似する非負テンソルが手に入る．テンソルのランクの定義は以下を参照．

genkaiphd.hatenablog.com

Julia言語 高速非負値行列因子分解lraNMFを実装した．

すごく速くNMFができるらしい2012年の論文を実装しました．

ieeexplore.ieee.org

epsilon を 0 にするとロスがNaNになるので注意．しばしばロスがNaNになるので使うときはverbose=trueにして様子を見ること推奨．

using LinearAlgebra
using Random
using Arpack
Random.seed!(123)

function lranmf_mu(X, r ; max_iter=200, tol = 1.0E-3, verbose = false)
    # lranmf_mu is effective when r << min(n,m)
    # input is a onnegative matrix
    # proposed by Guoxu Zhou in 2012
    # https://ieeexplore.ieee.org/document/6166354

    n, m = size(X)
    epsilon = 0.0001

    # Step1 in section II-B.
    if r == min(n, m)
        svd_X = svd(X)
    else
        svd_X = svds(X; nsv=r, ritzvec=true)[1]
    end
    Achil = svd_X.U * diagm(svd_X.S)
    Bchil = svd_X.V

    # Step2 in section II-B.
    A = rand(n, r)
    B = rand(m, r)
    cost_at_init = norm(X - A*B')
    previous_cost = cost_at_init
    for iter = 1:max_iter
        B .= B .* ( max.( Bchil*(Achil' * A), epsilon ) ) ./ ( B*(A'*A) )
        A .= A .* ( max.( Achil*(Bchil' * B), epsilon ) ) ./ ( A*(B'*B) )

        if tol > 0 && iter % 10 == 0
            cost = norm(X - A*B')
            if verbose
                println("iter: $iter cost: $cost")
            end
            if (previous_cost - cost) / cost_at_init < tol
                break
            end
            previous_cost = cost
        end
    end

    # A * B' is rank-r matrix
    return A, B'
end

これで速くなるのかとこないだ実装した普通のNMF(論文中のNMF_MU)と比較してみた． 普通のNMFの実装は以下．ロスはL2．乱数のseedを固定した．

using LinearAlgebra
using Random
using Arpack
Random.seed!(123)

function nmf_euc(X, r ; max_iter=200, tol = 1.0E-3, verbose = false)
    m, n = size(X)
    W = rand(m, r)
    H = rand(r, n)

    error_at_init = norm(X - W*H)
    previous_error = error_at_init
    for iter = 1:max_iter
        H .=  H .* ( W' * X ) ./ ( W' * W * H  )
        W .=  W .* ( X  * H') ./ ( W  * H * H' )

        if tol > 0 && iter % 10 == 0
            error = norm(X - W*H)
            if verbose
                println("iter: $iter cost: $error")
            end
            if (previous_error - error) / error_at_init < tol
                break
            end
            previous_error = error
        end
    end

    return W, H
end


function main()
    X = rand(5000, 5000)
    r = 5
    mxcnt = 10

    runtime = 0.0
    loss = 0.0
    for i = 1:mxcnt
        runtime += @elapsed begin
            A, B = nmf_euc(X, r, verbose=false, tol=1.0E-4)
        end
        loss += norm(X-A * B)
    end
    ave_runtime = runtime / mxcnt
    ave_loss = loss / mxcnt
    println("nmf_euc runtime $ave_runtime")
    println("nmf_euc loss $ave_loss")

    runtime = 0.0
    loss = 0.0
    for i = 1:mxcnt
        runtime += @elapsed begin
            A, B = lranmf_mu(X, r, verbose=false, tol=1.0E-4)
        end
        loss += norm(X - A * B)
    end
    ave_runtime = runtime / mxcnt
    ave_loss = loss / mxcnt
    println("lranmf runtime $ave_runtime")
    println("lranmf loss $ave_loss")

end

main()

mxcnt回繰り返して，経過時間の平均をとってる．lossの評価は，本当はこんな雑にはかっちゃだめだけど，乱数シード固定しているから，まぁいいでしょう．結果．

nmf_euc runtime 35.48805575
nmf_euc loss 1443.2935317424924
lranmf runtime 9.62555351
lranmf loss 1444.506586518955

ターゲットランクrが小さいとlraNMF_muが十分に速いことがわかった．なので，rが小さい場合は，lra-NMFを使えば良いのではないでしょうか！ちなみにtol=1.0E-3くらいだとあんまり大差ない．

Julia言語 テンソルのKLダイバージェンス, αダイバージェンス

この論文の式(8)の実装になんと午前中を全て費やしてしまった...

Nonnegative Tucker decomposition with alpha-divergence - IEEE Conference Publication

テンソルの計算は慣れないなぁ． α=0,1でKLダイバージェンスになるんだけど，テンソルに対するKLダイバージェンスの定義はこの論文の式(15)を採用した．ところでなんでKLダイバージェンスのことをIダイバージェンスって読んでるの？あとLSエラーのLSってなんだ

とりあえずテンソルの足の添え字集合を用意する関数をつくっておく．こーゆのつくらずにうまいことできればいいんだけどなぁ．この関数は，こちらのWebページを参考にした．直積集合をもっと気軽につくれるようにしたい．

function get_tensor_idxs(args...)
    if length(args) == 0
        [[]]
    else
        xs = [[x,] for x = 1:args[1]]
        for i = 2 : length(args)
            xs = [[x..., y] for x = xs for y = 1:args[i]]
        end
        xs
    end
end

あとは定義にしたがって実装するだけ．

function D_KL(X, Xhat)
    # Tensor of KL-divergence is defined as
    # I-divergence in eq(15) in
    # http://mlg.postech.ac.kr/~seungjin/publications/cvpr07.pdf

    d_kl = 0.0

    input_tensor_shape = size(X)
    idxs = get_tensor_idxs(input_tensor_shape...)
    for idx in idxs
        d_kl += X[idx...] * log( X[idx...] / Xhat[idx...] )
    end
    d_kl -= sum(X)
    d_kl += sum(Xhat)

    return d_kl
end

function D_alpha(X, Xhat, alpha)
    # D_alpha(X, Xhat, 1) = D_KL(X, Xhat)
    # D_alpha(X, Xhat, 0) = D_KL(Xhat, X)
    if alpha == 1
        return D_KL(X, Xhat)
    end
    if alpha == 0
        return D_KL(Xhat, X)
    end

    d_alpha = 0.0
    d_alpha += alpha * sum(X)
    d_alpha += (1.0 - alpha) * sum(Xhat)

    input_tensor_shape = size(X)
    idxs = get_tensor_idxs(input_tensor_shape...)
    for idx in idxs
        d_alpha -= X[idx...]^alpha * Xhat[idx...]^(1.0 - alpha)
    end

    return d_alpha / (alpha - alpha^2)
end

追記

Juliaでテンソルの足のインデックスが欲しい時はCartesianIndicesを使うと良いみたい．強い人に教わった．もっと早く知りたかった．．

Julia言語 配列の全要素が同じか判定する．

Julia言語で配列の全要素が同じかどうか調べる方法をぐぐってみると，

stackoverflow.com

まぁ，こんな感じのが出てきて，私は怠惰なので，自前で関数かくのが．ぶっちゃけだるいなと，ツイッターで呟いたら強い人が「Setにして要素数を数えたらいいんじゃね？」と教えてくれた．

ふむふむ

X = [1,2,3,4]
length(Set(X))
# 4

X = [1,1,1,1]
length(Set(X))
# 1

なるほど．加えて，強い人が，isequalを使えばよい！と教えてくれた．

X = [1,1,1,1]
all(isequal(first(X)),X)
# true

要は全要素が初めの要素と等しいか判別するわけですね，とってもスマート！

Julia言語 αβダイバージェンスでの非負値行列因子分解

αダイバージェンスやβダイバージェンスでのNMFを一般化するために，αβダイバージェンスというものを定義します．入力行列と出力低ランク行列間のαβダイバージェンスが小さくなるようなNMFアルゴリズムをJuliaで実装しました．αβダイバージェンスやアルゴリズムは以下の論文の通りに実装しました．

Entropy | Free Full-Text | Generalized Alpha-Beta Divergences and Their Application to Robust Nonnegative Matrix Factorization

あんまりちゃんとテストしてないので，使うときは気を付けてね． とりあえず，αβダイバージェンスD_abを定義に従って計算できるようにD_ab関数を用意しておく．α=β=1で通常のフロベニウスノルムになる．

using LinearAlgebra

function D_KL(P, Q)
    n, m = size(P)
    d_kl = 0.0
    for i = 1:n
        for j = 1:m
            d_kl += P[i,j] * log( P[i,j] / Q[i,j] ) - P[i,j] + Q[i,j]
        end
    end
    return d_kl
end

function D_IS(P, Q)
    #Itakura-Saito distance

    n, m = size(P)
    d_is = 0.0
    for i = 1:n
        for j = 1:m
            d_is += log( Q[i,j] / P[i,j] ) + P[i,j] / Q[i,j] + - 1.0
        end
    end
    return d_is
end

function D_logeuc(P, Q)
    n, m = size(P)
    log_P = log.(P)
    log_Q = log.(Q)
    return sum( (log_P - log_Q).^2 )
end

function D_ab(P, Q, alpha, beta)
    # defined by Andrzej Cichocki in
    # Entropy2011,13, 134-170; doi:10.3390/e13010134OPEN
    # See also equation (23) in
    # core.ac.uk/download/pdf/51394763.pdf
    # D_ab = D_euc when alpha = 1 and beta = 1

    if alpha != 0 && beta == 0
        return 1.0 / alpha^2 * D_KL(P.^alpha, Q.^beta)
    end
    if alpha + beta == 0 && alpha !=0 && beta !=0
        return 1.0 / alpha^2 * D_IS(P.^alpha, Q.^alpha)
    end
    if alpha == 0 && beta != 0
        return 1.0 / beta^2 * D_KL(Q.^beta, P.^beta)
    end
    if alpha == 0 && beta == 0
        return 1.0 / 2.0 * D_logeuc(P, Q)
    end

    n, m = size(P)
    d_ab = 0.0
    for i = 1:n
        for t = 1:m
            d_ab += P[i,t]^alpha * Q[i,t]^beta
            d_ab += -alpha / (alpha + beta) * P[i,t]^(alpha+beta)
            d_ab +=  -beta / (alpha + beta) * Q[i,t]^(alpha+beta)
        end
    end

    return -1.0 * d_ab / (alpha*beta)

end

あとは論文の更新ルールをそのまま実装する．

function nmf(P, r ; alpha=1, beta=1, max_iter=200, tol = 1.0E-3, verbose = false)
    # proposed by Andrzej Cichocki in
    # Entropy2011,13, 134-170; doi:10.3390/e13010134OPEN
    # See also equation (69) and (70) in
    # core.ac.uk/download/pdf/51394763.pdf
    #
    # (alpha, beta) = (1.0, 1.0) is usual euc-NMF
    # (alpha, beta) = (1.0, 0.0) is KL-NMF
    # (alpha, beta) = (0.0, 1.0) is IS-NMF

    n, m = size(P)
    A = rand(n, r)
    X = rand(r, m)
    one_mn = ones(n, m)

    error_at_init = D_ab(X, A*X, alpha, beta)
    previous_error = error_at_init
    for iter in 1:max_iter
        # update rule eq(69)
        Q = A*X
        Z = P.^alpha .* Q.^( beta-1 )
        X .= X .* ( (A'*Z) ./ (A'*Q.^(alpha+beta-1))).^(1.0/alpha)


        # update rule eq(70)
        Q = A*X
        Z = P.^alpha .* Q.^( beta-1 )
        A .= A .* ( (Z*X') ./ (Q.^(alpha+beta-1) * X')).^(1.0/alpha)


        if tol > 0 && iter % 10 == 0
            error = D_ab(P, A*X, alpha, beta)
            if verbose
                println("iter: $iter cost: $error")
            end
            if (previous_error - error) / error_at_init < tol
                break
            end
            previous_error = error
        end
    end

    return A, X
end

A*Xが入力行列Pを近似するrランク行列となる．

追記

私の記憶が正しければKL-NMFは行和列和を保持する．しかし，このアルゴリズムでα=1,β=0にしても行和列和が保持されない．何か間違えていると思う．そもそも論文の式(71)なんかおかしい気がするのは気のせいだろうか．

追記2

以前アップロードしたNMFの記事のコードと，上のコードとで同じ行列を入れても別の答えが返ってくる．やはりこの実装あやしい．．．（さすがに論文が間違っている可能性は低いと思うので，私の実装がおかしいのだろう．．．）

genkaiphd.hatenablog.com

追記3

α=1, β=0で更新式が以前の記事で引用した文献にある式にならない．Normalize Factor分ずれている気がする．めんどくさいが，今度，自分で更新式を導いて，どこが怪しいか調べる．

Julia言語でランダムウォーク

小針先生の確率統計の本を読んだ．教訓がたくさん詰まった本当に良い本だったと思う．６章の「酔歩」がとても印象に残っている．独立した章なので，確率の基本的なことが分かっていれば読める．

時刻t=0で原点に居る酔っ払いが，確率1/2で西へ，確率1/2で東に一歩進むランダムウォークを考えると，原点付近をうろちょろしそうだけど，まぁ，冷静に考えればそんなことはない．Juliaで酔っぱらいを召喚して，実験してみる．

function random_walker(n_steps)
    traj = [0]
    for step = 1 : n_steps
        coin = rand()
        pos = traj[step]
        if coin > 0.5
            append!(traj, pos + 1)
        else
            append!(traj, pos - 1)
        end
        println("step: $step pos: $pos")
    end
    return traj
end

trajに各ステップでの酔っぱらいの位置が保存される．とりあえず酔っぱらいを5人くらい召喚しよう．

using Plots
function main(n_walkers)
    n_steps = 30000

    fnt = font(16, "times")
    p_r = plot(legend = :topleft)
    for walker = 1:n_walkers
        traj = random_walker(n_steps)
        plot!(p_r, [1:n_steps+1;], traj,
            xlabel      = "step",
            ylabel      = "pos",
            xguidefont  = fnt,
            yguidefont  = fnt,
            xtickfont   = fnt,
            ytickfont   = fnt,
            titlefont   = fnt,
            title       = "trajectory of radom walkers",
            size        = (1200, 600),
            linewidth   = 3,
            label       = "random_walker $walker")
    end
    plot!([0.0], st=:hline, label=false)
    savefig(p_r, "traj_rw.png")
end

main(5)

これをプロットしてみる．横軸がステップ数，縦軸が酔っぱらいの位置である．

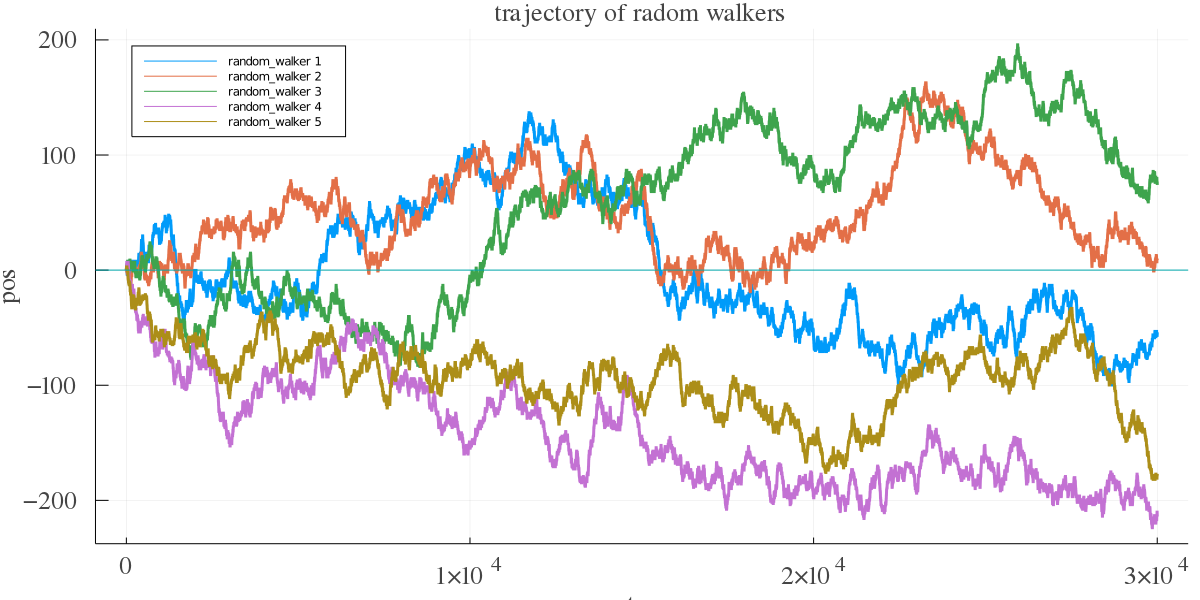
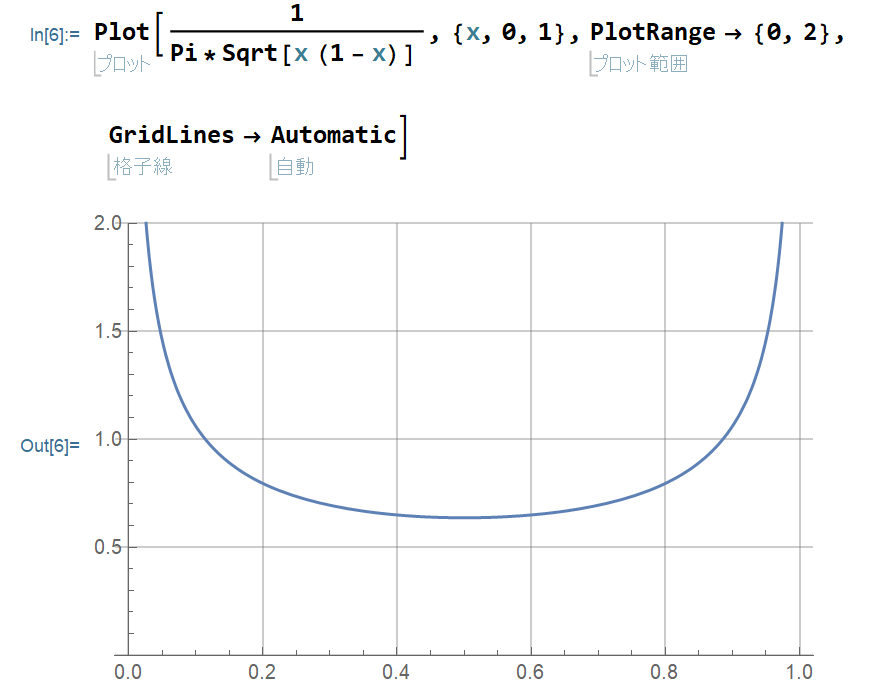
観ての通り，原点付近をうろちょろしているわけじゃない．実は，単位時間あたりに原点より東に居る時間をx，西に居る時間を1-xとすると，この分布は

p(x) = (π√(x(1-x)))^-1

になって，東か西かのどちらか片方ばかりに多くいる確率の方が大きい．

また，どんなに長い時間観測しても，「１度も原点に戻らない」確率と「１度しか原点に戻らない」確率が最も大きく，m回復帰する確率は，mが大きいほど小さいことが示せる．この話は，小針先生の「確率・統計入門」の第6章「酔歩」に証明を含め詳しく議論されてる．古い本だけど，とても読みやすい．独特の言い回しで著者の息遣いが聞こえてくるすごい良い本だと思う．例えば，このランダムウォークに関して小針先生は

正の領域に居る時は善行，負の領域に居る時は悪行を行っている時間とすると，善悪半々というマジメ人間は最も少く，悪い奴ほどはびこり，あるいは善人ほど多いということなのである．これは真実かもしれない p148

とか，

原点のまわりをウロウロするという最初の予想に反して，それほどセンチメンタルに故郷を慕うのではない p154

とかしゃれたことを言うのである．楽しい．

特に最初の第一章は「円に任意の弦をひくとき，その長さが内接正三角形の一片より長くなる確率を求めよ」という例題に対してA君B君C君の異なる回答の総括として，

真理というものがどこかにあって、それを探究するのが学問、ではなくて、何を仮定すれば何が結論されるかの論理の連鎖が学問である。

と言っていて，読んでて興奮するものがある．

どうやら小針先生はこの本を完成させることなく急逝し，旧友たちがこの本を完成させたようである．この本の前書きやあとがきには，なかなかドラマを感じるので，本屋で見かけたらぜひ手に取ってみたらどうだろう．

全然関係ないけど，酔歩つながりで，「酔歩する男」っていう物語がある．玩具修理者に収録されている．これがなかなか鳥肌の立つよいタイムリープ系SFで面白いのです．

Julia言語 αダイバージェンスで非負値行列因子分解

こないだのJuliaでNMFしたコードを一般のαダイバージェンスの尺度でNMFできるようにしました． αダイバージェンスの定義はここを参考にしました． 更新式はこの論文の2節に書いてあります．なんと更新式の一部をα倍したり1/α倍したりするだけ，簡単！

using LinearAlgebra
using Random
Random.seed!(123)

function D_KL(A, B)
    n, m = size(A)
    kl = 0.0
    for i = 1:n
        for j = 1:n
            kl += A[i,j] * log( A[i,j] / B[i,j] ) - A[i,j] + B[i,j]
        end
    end
    return kl
end

function D_alpha(A, B, alpha)
    # D_alpha(A, B, 1) = D_KL(A, B)
    # D_alpha(A, B, 0) = D_KL(B, A)
    if alpha == 1
        return D_KL(A, B)
    end
    if alpha == 0
        return D_KL(B, A)
    end

    A = A / sum(A)
    B = B / sum(B)

    n, m = size(A)
    d_alpha = 0.0
    for i = 1:n
        for j = 1:m
            d_alpha += alpha * A[i,j] + (1-alpha) * B[i,j] - X[i,j].^alpha * B[i,j].^(1-alpha)
        end
    end
    return 1.0 / ( alpha - alpha^2 ) * d_alpha
end

function nmf_alpha(X, r, alpha; max_iter=200, tol = 0.000001)
    m, n = size(X)
    W = rand(m, r)
    H = rand(r, n)
    one_mn = ones(m, n)

    error_at_init = D_alpha(X, W*H, alpha)
    previous_error = error_at_init
    for iter in 1:max_iter
        H .=  H .*( ( W' * ( X ./ (W*H) ).^alpha) ./ ( W' * one_mn )).^(1.0/alpha)
        W .=  W .*( ( ( X ./ (W*H) ).^alpha * H') ./ ( one_mn * H' )).^(1.0/alpha)

        if tol > 0 && iter % 10 == 0
            error = D_alpha(X, W*H, alpha)
            if (previous_error - error) / error_at_init < tol
                break
            end
            previous_error = error
        end
    end

    return W, H
end

こーゆのってどうやってテストすればいいんでしょうね． sklearnにはαダイバージェンスでNMFは実装されてないみたいなので結果を比較できなかった．更新式の一部をα倍するだけなので，pythonでも比較的容易に実装できると思う． そのうちついでにJuliaでβダイバージェンスでNMFも実装しておきたいな．

そろそろ研究で必要なので非負テンソル因子分解を実装しないといけない．．．

Julia言語 適当な分布に従うテンソルをつくる

各要素が適当な分布に従うテンソルをつくる．例えば，中心がmu, 分散がsigmaの一次元ガウス分布に各要素が従うD×M×Nテンソルをつくりたければ

using Distributions

mu = 0
sigma = 5
D = 2
M = 3
N = 5
dist = Normal(mu, sigma)
X = rand( dist, (D, M, N) )

とすればいい．

Julia言語 手っ取り早く B = { b ∈ {±1}^N } を生成する方法

集合 B ={ b ∈ {±1}^N } を得たい！ 僕が考えたのはこんな感じ．

using Combinatorics

function main(N)
    B=[]
    for n=1:N
        combs = collect(combinations(1:N,n))
        for comb in combs
            b = ones(N)
            for com in comb
                b[com] = -1
            end
            push!(B,b)
        end
    end
    return B
end

B = main(5)

display(B)

これを実行すれば

 [1.0, 1.0, 1.0, 1.0, 1.0]
 [-1.0, 1.0, 1.0, 1.0, 1.0]
 [1.0, -1.0, 1.0, 1.0, 1.0]
 [1.0, 1.0, -1.0, 1.0, 1.0]
 [1.0, 1.0, 1.0, -1.0, 1.0]
 [1.0, 1.0, 1.0, 1.0, -1.0]
 [-1.0, -1.0, 1.0, 1.0, 1.0]
 [-1.0, 1.0, -1.0, 1.0, 1.0]
 [-1.0, 1.0, 1.0, -1.0, 1.0]
 [-1.0, 1.0, 1.0, 1.0, -1.0]
 [1.0, -1.0, -1.0, 1.0, 1.0]
 [1.0, -1.0, 1.0, -1.0, 1.0]
 [1.0, -1.0, 1.0, 1.0, -1.0]
 [1.0, 1.0, -1.0, -1.0, 1.0]
 [1.0, 1.0, -1.0, 1.0, -1.0]
 [1.0, 1.0, 1.0, -1.0, -1.0]
 [-1.0, -1.0, -1.0, 1.0, 1.0]
 [-1.0, -1.0, 1.0, -1.0, 1.0]
 [-1.0, -1.0, 1.0, 1.0, -1.0]
 [-1.0, 1.0, -1.0, -1.0, 1.0]
 [-1.0, 1.0, -1.0, 1.0, -1.0]
 [-1.0, 1.0, 1.0, -1.0, -1.0]
 [1.0, -1.0, -1.0, -1.0, 1.0]
 [1.0, -1.0, -1.0, 1.0, -1.0]
 [1.0, -1.0, 1.0, -1.0, -1.0]
 [1.0, 1.0, -1.0, -1.0, -1.0]
 [-1.0, -1.0, -1.0, -1.0, 1.0]
 [-1.0, -1.0, -1.0, 1.0, -1.0]
 [-1.0, -1.0, 1.0, -1.0, -1.0]
 [-1.0, 1.0, -1.0, -1.0, -1.0]
 [1.0, -1.0, -1.0, -1.0, -1.0]
 [-1.0, -1.0, -1.0, -1.0, -1.0]

となって，所望の集合Bを得る．

これで，めでたしめでたしなのだが，もっと良い方法を強い人に教えてもらった．

a = [-1, 1]
B = vec(collect(Iterators.product(fill(a,4)...)))

これでも同じものが手に入る．Iteratorsを使いこなせるようになりたい．

また，他の強い人に，bit探索のノリでいけるんじゃないの？というコメントを貰いました．

for i in 0:2^N-1
    ptn = digits(i, base=2, pad=N)
    println(ptn)
end

所望のBにしたかったら，2倍して，1を引けばよい．これ，とても速い気がするんだけど，どうなんだろう．

そんなことせずに，無名関数でどうにかなることを知りました．

arr = [-1,1]
for i in 0:2^N-1
    ptn = digits(i, base=2, pad=N)
    println( (d -> arr[d+1]).(ptn) )
end

また，他の強い人によると，このように１行で済ませることもできるみたいです．

[[(-1)^parse(Int,string(i, base=2,pad=5)[k]) for k=1:5] for i=0:2^5-1 ]

また，他の強い人によると，map関数をうまく使えばもっとスマートのようです．

[map(x->2x-1, digits(i,base=2,pad=N)) for i in 0:2^(N)-1]

また，他の強い人によると，このようにもできるみたいです．

n = 4
[[(-1)^(i >> k & 1) for k in 0:n-1 ] for i in 1:2^n]