自分が勉強するのに役に立ったYoutubeで公開されている講義をどんどん追加していきます.
数学
松本多様体の内容を(かなり端折りながらも)丁寧に追っていく授業です.理解が深まりました.面白かった.
確率過程論を測度論、積分論を前提にせずに授業してくれているありがたい授業.
まだ観てないが,代数についての講義っぽい.
まだ観てないが,代数についての講義っぽい.ガロア理論に追いつくには良いかも?
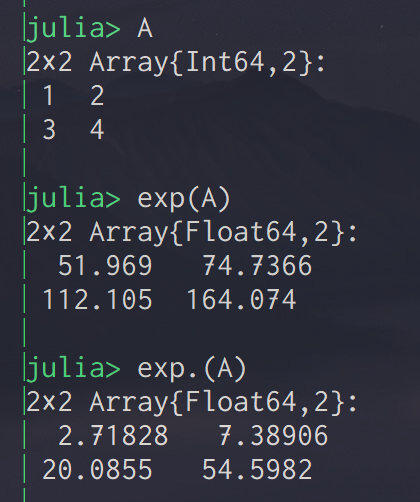
計算機科学
物性物理学
修士課程の時に何度も繰り返しみた講義です.ベリー位相や物性のトポロジカルな性質などが非常に良くまとまっています.私が修士の時は,この辺りは優れた日本語の教科書がなかったので,この講義にはかなり助けられました.
Youtuber
式変形チャンネル ゼロから始める群論2020
式変形チャンネル 群論シリーズ ~群の定義から準同型定理まで~
Masaki Koga [数学解説] 具体例で学ぶ代数学《群論》
AIcia Solid Project ブラックショールズ方程式への道 9講